Станция страховки и нагрузки, действующие на нее при срыве

Предлагаю поговорить на одну из самых актуальных тем — сила нагрузки на станцию страховки при срыве. Причина, по которой я решила открыть эту тему — бурный спор с моим другом. Прочтя много разной литературы, потратив пару ночей на просчеты математических формул и выслушав мнение некоторых опытных альпинистов, мы по-прежнему остались при разных мнениях.

Собственно спор начался с утверждения о том, что если лезущий вышел с нижней страховкой выше станции (например на 10 метров) и сорвался, то сила нагрузки на станцию будет одинакова, если бы он вышел выше станции всего на 1-2 метра.

В этом споре присутствовали обязательные условия:

— лидирующий лезет с динамической веревкой;

— при срыве лидера — выше станции нет не одной промежуточной точки страховки;

— рельеф должен быть достаточно вертикальным, чтобы не создавалось трение о скалу при падении, за счет которого нагрузка на станцию пришлась бы меньше.

Спор зашел в тупик…

Мое утверждение следующее — человек при срыве с нижней страховкой выше станции на 10-15 метров, принесет большую нагрузку на станцию, чем если бы он сорвался, уйдя от станции выше всего на пару метров.

Утверждение моего оппонента — в обеих приведенных мной случаях, нагрузка на станцию будет совершенно одинаковой.

Вот официальные просчеты, которые помогут понять суть вопроса:

Взято отсюда: http://www.kuban.ru/tourism/clubs/edelweis/text6.html

Приведем вывод формулы, описывающей поведение альпинистской веревки при срыве первого в связке.

П= Р*(H+L+ΔL) — потенциальная энергия человека.

P

— вес человека (

P = mg

)

H

— превышение человека над последней точкой страховки

L

— длина свободной веревки

ΔL

— длина, на которую веревка максимально растянулась

Аторм.=Fторм.*Δs — работа сил трения в тормозном устройстве

Fторм.

— сила трения веревки в тормозном устройстве

Δs

— длина протравливания веревки

Учтем силы трения в карабине:

			F1= F-Fтрен. Fтрен = f*N = f*(F+F1) = f*( 2F -Fтрен.) Fтрен. = (2f/(1+f))*F , где f — коэффициент трения.
	Направление сорвавшегося, растяжение веревки — ΔL»		N=2F-Fтрен.=(2/(1+f))*F А трен.= (1/2)*Fтрен.*ΔL’ — работа сил трения в карабине (сила трения меняется линейно, одновременно с силой F, от нуля до максимального значения Fтрен., поэтому в формуле присутствует коэффициент 1/2 ).
Направление базы, растяжение веревки — ΔL’

ΔL= ΔL’+ΔL» — растяжение веревки складывается из растяжения веревки со стороны базы ΔL’ и растяжения веревки со стороны сорвавшегося ΔL».

Е= (1/2)*( F*ΔL» + F1*ΔL’) — энергия деформации веревки

E + Aтрен. = (1/2)*( F*ΔL» + F1*ΔL’) + (1/2)*Fтрен.*ΔL’;

E + Aтрен. = (1/2)*( F*ΔL» +(F-Fтрен.)* ΔL’ + Fтрен.*ΔL’) = (1/2)F*ΔL

F=α*(ΔL/Lo) — сила рывка (усилие деформации веревки )

α

— коэффициент упругости веревки

Lо

— общая длина ненагруженной веревки

ΔL= ΔL’+ΔL»=(1/α)*( F*L + F1*L1) = (1/α)*(F*L + (F-Fтрен.)*L1);

ΔL= (1/α)*(F*L + F*(1 — (2f /(1+f))*L1) = (1/α)*(F*L +F*L1- (2f/(1+f))*F*L1);

ΔL= (F*Lo/α)*(1- (2f/(1+f))(L1/Lo));

L1 — длина веревки между базой и верхней (последней) точкой

К=(H + L)/Lo — фактор рывка

П=E+Aтрен. + Аторм. — Из закона сохранения энергии следует, что потенциальная энергия человека П переходит в энергию деформации веревки E, и работу сил трения в карабине Aтрен. и работу сил трения в тормозном устройстве Aторм.

После подстановки предыдущих выражений в закон сохранения энергии получим:

Р*(H+L+ΔL)= (1/2)F*ΔL + Fторм.*Δs;

(1/2)F*ΔL — P*ΔL — P(H+L- (Fторм./P)*Δs) = 0, разделим выражение на Lo

(1/2)F*(ΔL/Lo) — P*(ΔL/Lo) — P((H+L)/Lo- (Fторм./P)*(Δs/Lo)) = 0;

(1/2)F*(ΔL/Lo) — P*(ΔL/Lo) — P(K- (Fторм./P)*(Δs/Lo)) = 0; (K— фактор рывка)

Подставим сюда полученное выражение для ΔL= (F*Lo/α)*( 1 — (2f/(1+f))*(L1/Lo))

= 0
Получаем следующее решение уравнения для F:
-Сила рывка веревки.
— рывок на карабин.
-рывок на базу (или страхующего).
-относительное удлинение веревки при величине рывка на веревку F.

Теперь рассчитаем время воздействия рывка на сорвавшегося и распределение этого рывка во времени. После срыва человек падает вниз и веревка начинает нагружаться, тормозя падение человека и действуя как амортизатор. На человека со стороны веревки действует силы:

F= -( α/Lo)*ΔL

— сила упругости веревки;

P=mg

— сила тяжести (

P

— вес человека).

Будем считать, что затухания нет. В этом случае уравнение движения запишется следующим образом:

m*(ΔL)» + (α/Lo)* (L = mg;

Решением данного дифференциального уравнения есть функция: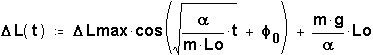
это косинусоида, смещенная на величину  (гармонические колебания).
Для величины силы упругости (рывка веревки) мы имеем следующую зависимость силы от времени:

-как видно — это тоже косинусоида.
— полупериод колебаний при рывке.
Fmax = — (α/Lo)*ΔLmax.
T/2           (время)

Рывок можно охарактеризовать временем воздействия на человека и элементы страховки — полупериодом косинусоиды. За это время сила рывка возрастает от нуля до максимума и снова уменьшается до нуля.

Надо еще заметить, что данное уравнение описывает поведение системы лишь при натянутой веревке. При движении в верхней части (положительный период косинусоиды) сила упругости на человека не действует и движение происходит только за счет силы тяжести ( L»= g , это движение по параболе ), но это не особо интересно для рассмотрения процесса страховки. После первого полупериода за счет диссипативных сил происходит уменьшение амплитуды колебаний (период не меняется). Если элементы страховочной цепи выдержали первый рывок, последующие не окажут существенного воздействия.

Время воздействия рывка нам интересно для оценки его жесткости: жесткость рывка тем выше, чем больше его сила и чем меньше время его воздействия. Короткий рывок оказывает более разрушающее воздействие, чем более плавный рывок , имеющий такую же силу.

***************************************************************

Вот еще материал: http://poxod.ru/equipment/safety/p_safety_zakmindelevichstrahovka_a.html

***************************************************************

Но сколько бы я не читала литературу, у меня остаются по-прежнему сомнения относительно бесспорного утверждения правильности просчетов в этих статьях. Тем-более, все они были написаны в советские времена, когда снаряжение значительно отличалось от современного. К тому же, практически везде больше говорится о нагрузке на веревку, а про станцию как-то вскользь. А ведь станция — это одно из важных условий соблюдения техники безопасности. Как ты ее организуешь — так и будет от этого зависеть ваша жизнь и жизнь напарника. Если говорить о стационарных точках страховки на станции (например шлямбурные крючья) тогда вопрос о надежности становится очевидным. А вот если станция организована исключительно на своих точках — в этом случае важен даже самый небольшой подсчет в силе нагрузке, которая приходится на станцию при рывке.

Надеюсь на вашу помощь, чтобы разобраться до конца в этом вопросе.

Источник: Проект ALP

Материал по теме: Что такое факторы рывка при срыве